2 Common Methods
2.1 Comparable vs. Comparator in Java
Comparable and Comparator are two interfaces provided by Java Core API. From their names, we can tell they may be used for comparing stuff in some way. But what exactly are they and what is the difference between them? The following are two examples for answering this question. The simple examples compare two HDTV's size. How to use Comparable vs. Comparator is obvious after reading the code.
2.1.1 Comparable
Comparable is implemented by a class in order to be able to comparing object of itself with some other objects. The class itself must implement the interface in order to be able to compare its instance(s). The method required for implementation is compareTo(). Here is an example:
class HDTV implements Comparable<HDTV> {
private int size;
private String brand;
public HDTV(int size, String brand) {
this.size = size;
this.brand = brand;
}
public int getSize() {
return size;
}
public void setSize(int size) {
this.size = size;
}
public String getBrand() {
return brand;
}
public void setBrand(String brand) {
this.brand = brand;
}
@Override
public int compareTo(HDTV tv) {
if (this.getSize() > tv.getSize())
return 1;
else if (this.getSize() < tv.getSize())
return -1;
else
return 0;
}
}
public class Main {
public static void main(String[] args) {
HDTV tv1 = new HDTV(55, "Samsung");
HDTV tv2 = new HDTV(60, "Sony");
if (tv1.compareTo(tv2) > 0) {
System.out.println(tv1.getBrand() + " is better.");
} else {
System.out.println(tv2.getBrand() + " is better.");
}
}
}
Sony is better.
2.1.2 Comparator
In some situations, you may not want to change a class and make it comparable. In such cases, Comparator can be used if you want to compare objects based on certain attributes/fields. For example, 2 persons can be compared based on height or age etc. (this can not be done using comparable.)
The method required to implement is compare(). Now let's use another way to compare those TV by size. One common use of Comparator is sorting. Both Collections and Arrays classes provide a sort method which use a Comparator.
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
class HDTV {
private int size;
private String brand;
public HDTV(int size, String brand) {
this.size = size;
this.brand = brand;
}
public int getSize() {
return size;
}
public void setSize(int size) {
this.size = size;
}
public String getBrand() {
return brand;
}
public void setBrand(String brand) {
this.brand = brand;
}
}
class SizeComparator implements Comparator<HDTV> {
@Override
public int compare(HDTV tv1, HDTV tv2) {
int tv1Size = tv1.getSize();
int tv2Size = tv2.getSize();
if (tv1Size > tv2Size) {
return 1;
} else if (tv1Size < tv2Size) {
return -1;
} else {
return 0;
}
}
}
public class Main {
public static void main(String[] args) {
HDTV tv1 = new HDTV(55, "Samsung");
HDTV tv2 = new HDTV(60, "Sony");
HDTV tv3 = new HDTV(42, "Panasonic");
ArrayList<HDTV> al = new ArrayList<HDTV>();
al.add(tv1);
al.add(tv2);
al.add(tv3);
Collections.sort(al, new SizeComparator());
for (HDTV a : al) {
System.out.println(a.getBrand());
}
}
}
output:
Panasonic
Samsung
Sony
Often we may use Collections.reverseOrder() method to get a descending order Comparator. Like the following:
ArrayList<Integer> al = new ArrayList<Integer>();
al.add(3);
al.add(1);
al.add(2);
System.out.println(al);
Collections.sort(al);
System.out.println(al);
Comparator<Integer> comparator = Collections.reverseOrder();
Collections.sort(al,comparator);
System.out.println(al);
Output:
[3,1,2]
[1,2,3]
[3,2,1]
2.1.3 When to use Which?
In brief, a class that implements Comparable will be comparable, which means it instances can be compared with each other.
A class that implements Comparator will be used in mainly two situations:
- It can be passed to a sort method, such as
Collections.sort()orArrays.sort(), to allow precise control over the sort order - It can also be used to control the order of certain data structures, such as sorted sets (e.g.
TreeSet) or sorted maps (e.g.,TreeMap).
For example, to create a TreeSet. We can either pass the constructor a comparator or make the object class comparable.
Approach 1 - TreeSet(Comparator comparator)
class Dog {
int size;
Dog(int s) {
size = s;
}
}
class SizeComparator implements Comparator<Dog> {
@Override
public int compare(Dog d1, Dog d2) {
return d1.size - d2.size;
}
}
public class ImpComparable {
public static void main(String[] args) {
TreeSet<Dog> d = new TreeSet<Dog>(new SizeComparator()); // pass comparator
d.add(new Dog(1));
d.add(new Dog(2));
d.add(new Dog(1));
}
}
Approach 2 - Implement Comparable
class Dog implements Comparable<Dog>{
int size;
Dog(int s) {
size = s;
}
@Override
public int compareTo(Dog o) {
return o.size - this.size;
}
}
public class ImpComparable {
public static void main(String[] args) {
TreeSet<Dog> d = new TreeSet<Dog>();
d.add(new Dog(1));
d.add(new Dog(2));
d.add(new Dog(1));
}
}
2.2 Java equals() and hashCode() Contract
The Java super class java.lang.Object has two very important methods defined:
public boolean equals(Object obj)
public int hashCode()
They have been proved to be extremely important to understand, especially when user-defined objects are added to Maps. However, even advanced-level developers sometimes can't figure out how they should be used properly. In this post, I will first show an example of a common mistake, and then explain how equals() and hashCode contract works.
2.2.1 A common mistake
Common mistake is shown in the example below.
import java.util.HashMap;
public class Apple {
private String color;
public Apple(String color) {
this.color = color;
}
public boolean equals(Object obj) {
if (!(obj instanceof Apple))
return false;
if (obj == this)
return true;
return this.color.equals(((Apple) obj).color);
}
public static void main(String[] args) {
Apple a1 = new Apple("green");
Apple a2 = new Apple("red");
//hashMap stores apple type and its quantity
HashMap<Apple, Integer> m = new HashMap<Apple, Integer>();
m.put(a1, 10);
m.put(a2, 20);
System.out.println(m.get(new Apple("green")));
}
}
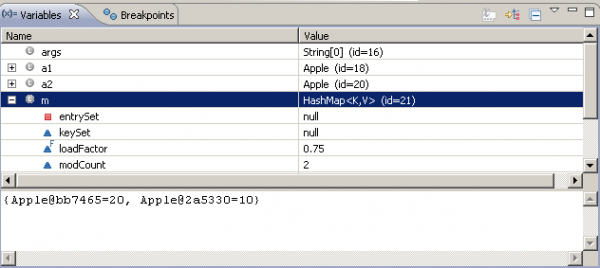
In this example, a green apple object is stored successfully in a hashMap, but when the map is asked to retrieve this object, the apple object is not found. The program above prints null. However, we can be sure that the object is stored in the hashMap by inspecting in the debugger:
2.2.2 Problem caused by hashCode()
The problem is caused by the un-overridden method "hashCode()". The contract between equals() and hasCode() is that:
- If two objects are equal, then they must have the same hash code.
- If two objects have the same hashcode, they may or may not be equal.
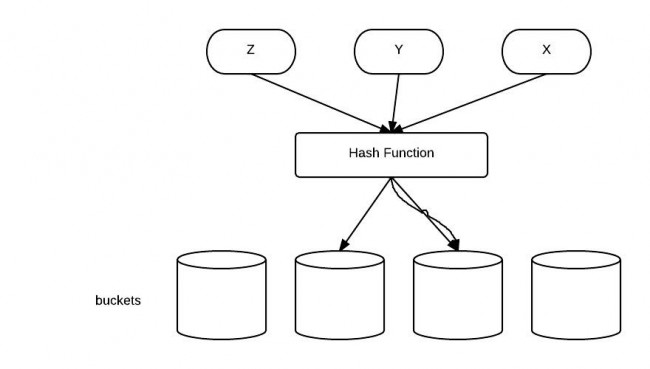
The idea behind a Map is to be able to find an object faster than a linear search. Using hashed keys to locate objects is a two-step process. Internally the Map stores objects as an array of arrays. The index for the first array is the hashcode() value of the key. This locates the second array which is searched linearly by using equals() to determine if the object is found.
The default implementation of hashCode() in Object class returns distinct integers for different objects. Therefore, in the example above, different objects(even with same type) have different hashCode.
Hash Code is like a sequence of garages for storage, different stuff can be stored in different garages. It is more efficient if you organize stuff to different place instead of the same garage. So it's a good practice to equally distribute the hashCode value. (Not the main point here though)
The solution is to add hashCode method to the class. Here I just use the color string's length for demonstration.
public int hashCode(){
return this.color.length();
}
2.3 Yet Another “Java Passes By Reference or By Value”?
This is a classic interview question which confuses novice Java developers. In this post I will use an example and some diagram to demonstrate that: Java is pass-by-value.
2.3.1 Some Definitions
Pass by value: make a copy in memory of the actual parameter's value that is passed in. Pass by reference: pass a copy of the address of the actual parameter.
Java is always pass-by-value. Primitive data types and object reference are just values.
2.3.2 Passing Primitive Type Variable
Since Java is pass-by-value, it's not hard to understand the following code will not swap anything.
swap(Type arg1, Type arg2) {
Type temp = arg1;
arg1 = arg2;
arg2 = temp;
}
2.3.3 Passing Object Variable
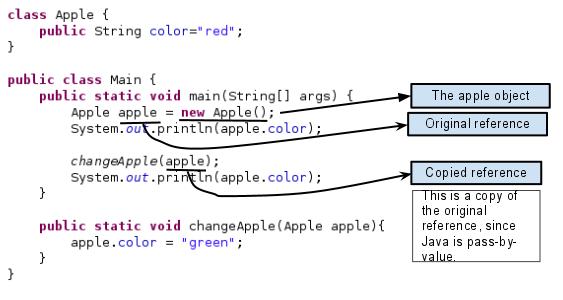
Java manipulates objects by reference, and all object variables are references. However, Java doesn't pass method arguments by reference, but by value.
Question is: why the member value of the object can get changed?
code:
class Apple {
public String color="red";
}
public class Main {
public static void main(String[] args) {
Apple apple = new Apple();
System.out.println(apple.color);
changeApple(apple);
System.out.println(apple.color);
}
public static void changeApple(Apple apple){
apple.color = "green";
}
}
Since the orignal and copied reference refer the same object, the member value gets changed.

output:
red
green
2.4 Iteration vs. Recursion in Java
2.4.1 Recursion
Consider the factorial function: n!=n*(n-1)*(n-2)*...*1
There are many ways to compute factorials. One way is that n! is equal to n*(n-1)!. Therefore the program can be directly written as:
Program 1:
int factorial (int n) {
if (n == 1) {
return 1;
} else {
return n*factorial(n-1);
}
}
n order to run this program, the computer needs to build up a chain of multiplications:factorial(n) → factorial(n-1) → factorial(n-2) → ... → factorial(1). Therefore, the computer has to keep track of the multiplications to be performed later on. This type of program, characterized by a chain of operations, is called recursion. Recursion can be further categorized into linear and tree recursion. When the amount of information needed to keep track of the chain of operations grows linearly with the input, the recursion is called linear recursion. The computation of n! is such a case, because the time required grows linearly with n. Another type of recursion, tree recursion, happens when the amount of information grows exponentially with the input. But we will leave it undiscussed here and go back shortly afterwards.
2.4.2 Iteration
A different perspective on computing factorials is by first multiplying 1 by 2, then multiplying the result by 3, then by 4, and so on until n. More formally, the program can use a counter that counts from 1 up to n and compute the product simultaneously until the counter exceeds n. Therefore the program can be written as:
Program 2:
int factorial (int n) {
int product = 1;
for(int i=2; i<n; i++) {
product *= i;
}
return product;
}
This program, by contrast to program 2, does not build a chain of multiplication. At each step, the computer only need to keep track of the current values of the product and i. This type of program is called iteration, whose state can be summarized by a fixed number of variables, a fixed rule that describes how the variables should be updated, and an end test that specifies conditions under which the process should terminate. Same as recursion, when the time required grows linearly with the input, we call the iteration linear recursion.
2.4.3 Recursion vs Iteration
Compared the two processes, we can find that they seem almost same, especially in term of mathematical function. They both require a number of steps proportional to n to compute n!. On the other hand, when we consider the running processes of the two programs, they evolve quite differently.
In the iterative case, the program variables provide a complete description of the state. If we stopped the computation in the middle, to resume it only need to supply the computer with all variables. However, in the recursive process, information is maintained by the computer, therefore "hidden" to the program. This makes it almost impossible to resume the program after stopping it.
2.4.4 Tree recursion
As described above, tree recursion happens when the amount of information grows exponentially with the input. For instance, consider the sequence of Fibonacci numbers defined as follows:
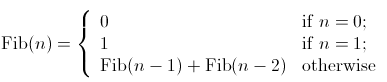
By the definition, Fibonacci numbers have the following sequence, where each number is the sum of the previous two: 0, 1, 1, 2, 3, 5, 8, 13, 21, ...
A recursive program can be immediately written as:
Program 3:
int fib (int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
return fib(n-1) + fib(n-2);
}
}
On the other hand, we can also write the program in an iterative way for computing the Fibonacci numbers. Program 4 is a linear iteration. The difference in time required by Program 3 and 4 is enormous, even for small inputs.
Program 4:
int fib (int n) {
int fib = 0;
int a = 1;
for(int i=0; i<n; i++) {
fib = fib + a;
a = fib;
}
return fib;
}
However, one should not think tree-recursive programs are useless. When we consider programs that operate on hierarchically data structures rather than numbers, tree-recursion is a natural and powerful tool. It can help us understand and design programs. Compared with Program 3 and 4, we can easily tell Program 3 is more straightforward, even if less efficient. After that, we can most likely reformulate the program into an iterative way.